It’s a Bluesky link but he use adult tags as de facto “spoiler” tags. The problem is that content is hidden if you’re not logged into Bluesky. Here’s a Bluesky mirror site to show the entire thread…
https://subium.com/profile/c0nc0rdance.bsky.social/post/3kpkcq2ecws22
A huge hint…
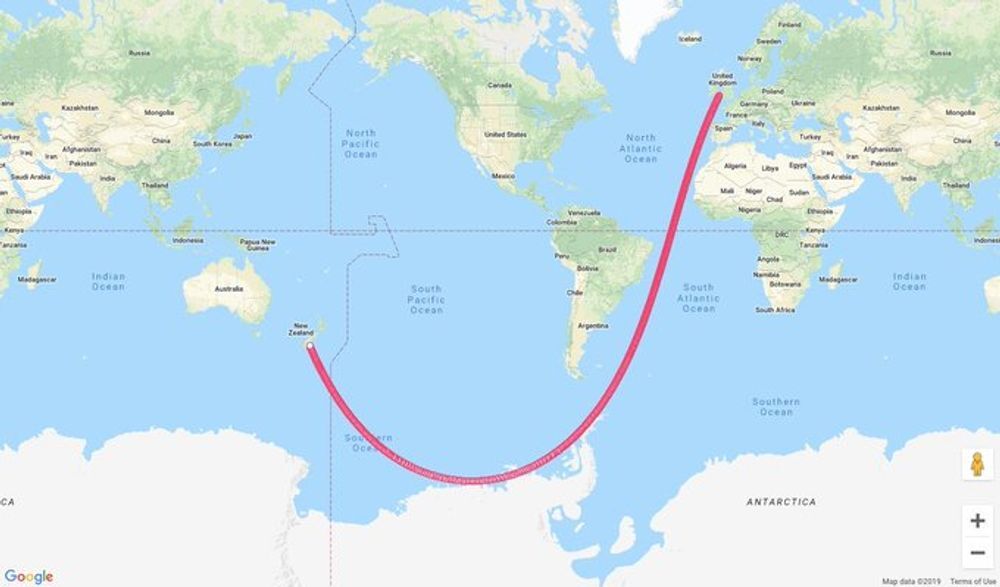


Also, you can define a geodesic for any surface, the concept isn’t specific to spheres.
Sorry, I shoul’ve said. The earth isn’t a sphere, ellipsoid, or other regular geometric shape. The ocean’s surface is less so and changes by the tides. Those shapes can work to model the surface locally and globally depending on accuracy needed but are inherently flawed.
Person 1: Does that matter? Person 2: No, let’s just simplify. Person 1: Ok, well we can really simplify using a Mercator projection. Person 2: You’re doing it wrong. We need to simplify the part that makes the line not straight, but not so much that it looks bendy again. Our projection needs to be at the level that makes the answer I want to be true look right. Person 1: Does the question even make any sense in this context then?
It doesn’t have to be a regular geometric shape. Any conceivable surface, no matter how awkward and lumpy — unless you have some infinitely rough mathematical object or other weird thing that doesn’t exist in real life — will permit the definition of geodesic curves.
But also, how much detail you account for is inherently a subjective decision tied to the level of precision you need for your specific application. Are you going to consider every whitecap and speck of foam when you describe your path? That depends! If your goal is to steer an ocean liner in a roughly straight line without hitting any landmasses, then probably not!
If you’re a satellite looking for sea-level defects due to gravitational anomalies, then you might need a little more precision.