Apr 17, 2017 Matt Brems writes:
Principal component analysis (PCA) is an important technique to understand in the fields of statistics and data science… but when putting a lesson together for my General Assembly students, I found that the resources online were too technical, didn’t fully address our needs, and/or provided conflicting information. It’s safe to say that I’m not “entirely satisfied with the available texts” here.
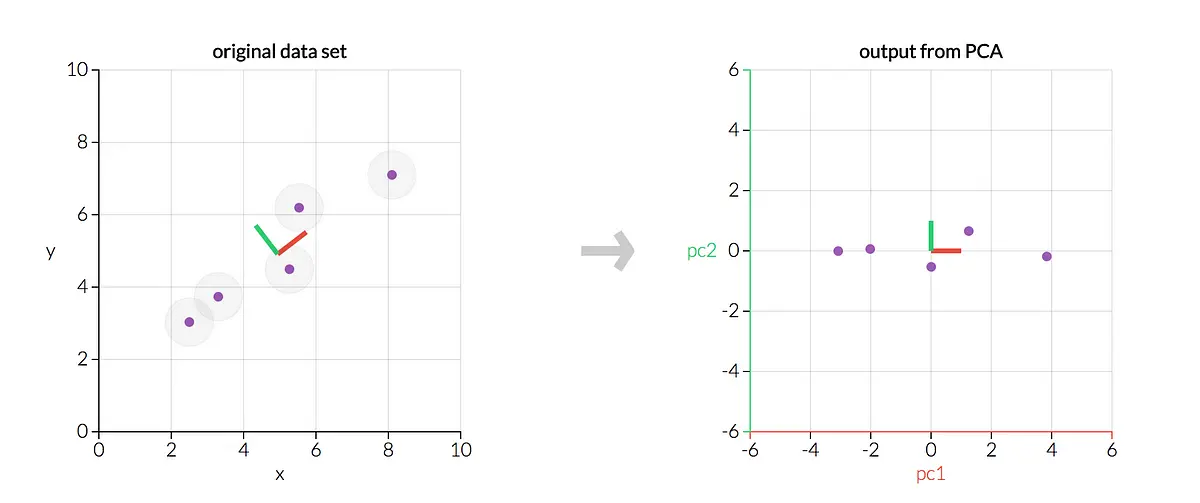
As a result, I wanted to put together the “What,” “When,” “How,” and “Why” of PCA as well as links to some of the resources that can help to further explain this topic. Specifically, I want to present the rationale for this method, the math under the hood, some best practices, and potential drawbacks to the method.
While I want to make PCA as accessible as possible, the algorithm we’ll cover is pretty technical. Being familiar with some or all of the following will make this article and PCA as a method easier to understand: matrix operations/linear algebra (matrix multiplication, matrix transposition, matrix inverses, matrix decomposition, eigenvectors/eigenvalues) and statistics/machine learning (standardization, variance, covariance, independence, linear regression, feature selection). I’ve embedded links to illustrations of these topics throughout the article, but hopefully these will serve as a reminder rather than required reading to get through the article.